幂函数: \(y = x^a\)
幂函数\(y = x^a\)(\(a\)为常数,\(x\)是自变量)的核心是“\(a\)决定一切”,不同\(a\)值对应不同的定义域、图像和性质,我们按“基础概念→分类性质→例题应用”的逻辑逐步拆解。
一、幂函数的核心定义
1. 表达式:严格形式为\(y = x^a\),其中自变量\(x\)在底数位置,常数\(a\)在指数位置,这是它与指数函数(如\(y = 2^x\),自变量在指数)的本质区别。
2. 定义域:由指数\(a\)的取值决定,没有统一范围,需根据\(a\)的类型(整数、分数、正数、负数)单独分析,比如\(a=2\)时\(x\)取全体实数,\(a=\frac{1}{2}\)时\(x\geq0\),\(a=-1\)时\(x\neq0\)。
3. 共性特征:所有幂函数的图像都必过点\((1,1)\),因为\(1\)的任何次幂都等于\(1\);但不一定过原点,比如\(a=-1\)时\(x=0\)无意义,图像就不过原点。
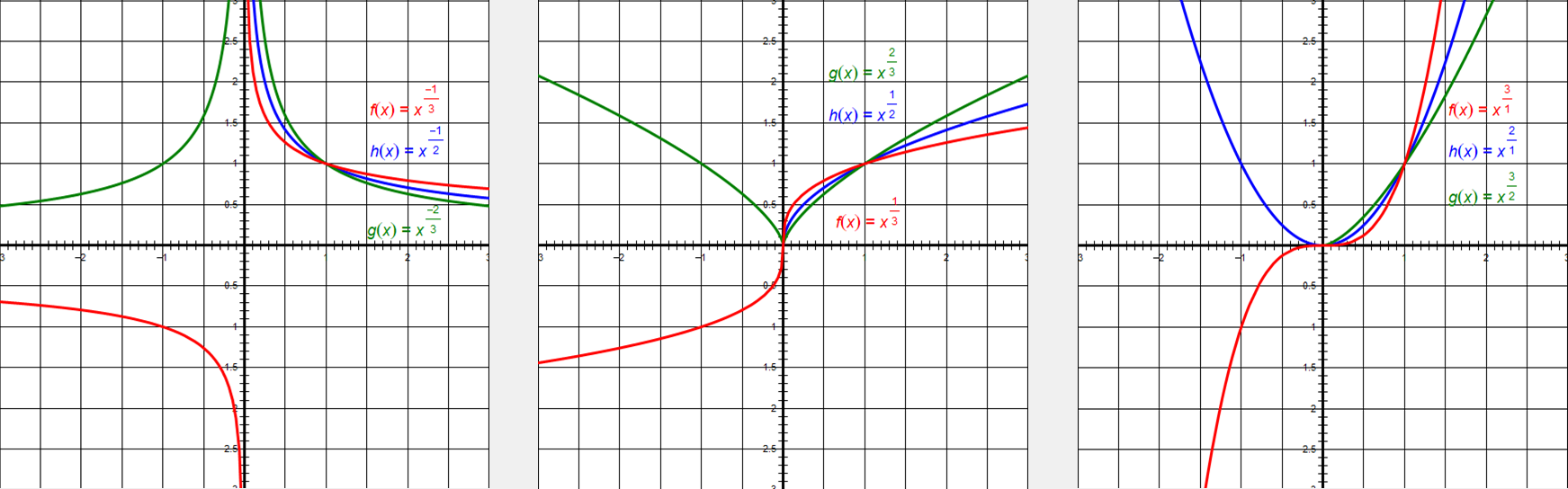
二、不同类型幂函数的性质(按\(a\)的取值分类)
我们按\(a\)的“正负”和“整数/分数”划分,这是最贴合解题需求的分类方式,每个类型的性质都从“定义域→值域→单调性→奇偶性→图像特征”展开。
1. 当\(a\)为正整数时(如\(a=1,2,3\))
定义域:全体实数(\(x\in\mathbb{R}\))。
值域:若\(a\)为奇数(如\(a=1,3\)),值域为全体实数;若\(a\)为偶数(如\(a=2,4\)),值域为非负数(\(y\geq0\))。
单调性:若\(a\)为奇数,在\(\mathbb{R}\)上单调递增(如\(y=x^3\),\(x\)越大\(y\)越大);若\(a\)为偶数,在\((-\infty,0]\)上单调递减,在\([0,+\infty)\)上单调递增(如\(y=x^2\),先减后增,顶点在原点)。
奇偶性:若\(a\)为奇数,是奇函数(图像关于原点对称,如\(y=x^3\));若\(a\)为偶数,是偶函数(图像关于\(y\)轴对称,如\(y=x^2\))。
图像特征:必过原点\((0,0)\)和\((1,1)\);\(a\)越大,在\(x>1\)的部分图像越“陡”(如\(y=x^3\)比\(y=x^2\)在\(x>1\)时上升更快)。
2. 当\(a\)为负整数时(如\(a=-1,-2\))
定义域:非零实数(\(x\in\mathbb{R}\)且\(x\neq0\)),因为负指数可转化为分式(\(x^{-n}=\frac{1}{x^n}\)),分母不能为0。
值域:若\(a\)为负奇数(如\(a=-1\)),值域为非零实数(\(y\in\mathbb{R}\)且\(y\neq0\));若\(a\)为负偶数(如\(a=-2\)),值域为正实数(\(y>0\))。
单调性:若\(a\)为负奇数(如\(y=x^{-1}=\frac{1}{x}\)),在\((-\infty,0)\)和\((0,+\infty)\)上分别单调递减(注意:不能说在全体定义域上递减,因为\(x=-1\)时\(y=-1\),\(x=1\)时\(y=1\),\(-1<1\)但\(-1<1\),不满足递减定义);若\(a\)为负偶数(如\(y=x^{-2}=\frac{1}{x^2}\)),在\((-\infty,0)\)上单调递增,在\((0,+\infty)\)上单调递减。
奇偶性:若\(a\)为负奇数,是奇函数(如\(y=\frac{1}{x}\),图像关于原点对称);若\(a\)为负偶数,是偶函数(如\(y=\frac{1}{x^2}\),图像关于\(y\)轴对称)。
图像特征:不过原点,必过\((1,1)\)和\((-1,\pm1)\)(\(a\)负奇数时\((-1,-1)\),负偶数时\((-1,1)\));图像分为两部分,分别在不同象限(\(a\)负奇数时在一、三象限,负偶数时在一、二象限),且与坐标轴无交点(因为\(x\)不能为0,\(y\)也不能为0)。
3. 当\(a\)为正分数时(如\(a=\frac{1}{2},\frac{2}{3}\),可表示为\(a=\frac{p}{q}\),\(p,q\)为正整数且互质)
定义域:若\(q\)为奇数(如\(a=\frac{2}{3}\),\(y=x^{\frac{2}{3}}=\sqrt[3]{x^2}\)),定义域为全体实数;若\(q\)为偶数(如\(a=\frac{1}{2}\),\(y=x^{\frac{1}{2}}=\sqrt{x}\)),定义域为非负数(\(x\geq0\)),因为偶数次根号下的数不能为负。
值域:若\(p\)为奇数、\(q\)为奇数(如\(a=\frac{1}{3}\),\(y=\sqrt[3]{x}\)),值域为全体实数;若\(p\)为偶数(无论\(q\)奇偶,如\(a=\frac{2}{3}\)或\(\frac{1}{2}\)),值域为非负数(\(y\geq0\))。
单调性:若\(q\)为奇数(如\(y=\sqrt[3]{x}\)),在\(\mathbb{R}\)上单调递增;若\(q\)为偶数(如\(y=\sqrt{x}\)),在\([0,+\infty)\)上单调递增。
奇偶性:仅当\(q\)为奇数时可能有奇偶性——若\(p\)为奇数(如\(a=\frac{1}{3}\)),是奇函数;若\(p\)为偶数(如\(a=\frac{2}{3}\)),是偶函数;若\(q\)为偶数(如\(a=\frac{1}{2}\)),定义域\(x\geq0\)不关于原点对称,非奇非偶。
图像特征:\(q\)为偶数时(如\(y=\sqrt{x}\)),图像仅在第一象限,过\((0,0)\)和\((1,1)\);\(q\)为奇数时(如\(y=\sqrt[3]{x^2}\)),图像过\((0,0)\)、\((1,1)\)和\((-1,1)\),关于\(y\)轴对称。
4. 当\(a\)为负分数时(如\(a=-\frac{1}{2},-\frac{2}{3}\),可表示为\(a=-\frac{p}{q}\),\(p,q\)为正整数且互质)
定义域:本质是\(y=x^{-\frac{p}{q}}=\frac{1}{\sqrt[q]{x^p}}\),所以需满足“根号下有意义”且“分母不为0”。若\(q\)为奇数(如\(a=-\frac{2}{3}\)),定义域为\(x\neq0\)的全体实数;若\(q\)为偶数(如\(a=-\frac{1}{2}\)),定义域为正实数(\(x>0\)),因为偶数次根号下非负且分母不为0。
值域:若\(q\)为奇数、\(p\)为奇数(如\(a=-\frac{1}{3}\),\(y=\frac{1}{\sqrt[3]{x}}\)),值域为\(y\neq0\)的全体实数;若\(p\)为偶数(无论\(q\)奇偶,如\(a=-\frac{2}{3}\)或\(-\frac{1}{2}\)),值域为正实数(\(y>0\))。
单调性:若\(q\)为奇数(如\(a=-\frac{1}{3}\)),在\((-\infty,0)\)和\((0,+\infty)\)上分别单调递减;若\(q\)为偶数(如\(a=-\frac{1}{2}\),\(y=\frac{1}{\sqrt{x}}\)),在\((0,+\infty)\)上单调递减。
奇偶性:仅当\(q\)为奇数时可能有奇偶性——若\(p\)为奇数(如\(a=-\frac{1}{3}\)),是奇函数;若\(p\)为偶数(如\(a=-\frac{2}{3}\)),是偶函数;若\(q\)为偶数(如\(a=-\frac{1}{2}\)),定义域\(x>0\)不关于原点对称,非奇非偶。
图像特征:不过原点,必过\((1,1)\);\(q\)为偶数时(如\(a=-\frac{1}{2}\)),图像仅在第一象限;\(q\)为奇数时(如\(a=-\frac{2}{3}\)),图像在一、二象限(\(p\)偶)或一、三象限(\(p\)奇),与坐标轴无交点。
例题1:判断下列函数是否为幂函数:①\(y=2x^3\);②\(y=x^2 + x\);③\(y=x^{-2}\);④\(y=(x-1)^4\)。
解析:
幂函数需满足“系数为1,底数仅为\(x\),无常数项或其他项”。①系数为2,不是;②含\(x^2\)和\(x\)两项,不是;③符合\(y=x^a\)(\(a=-2\)),是;④底数为\(x-1\),不是。
答案:③是幂函数。
例题2:求幂函数\(y=x^{\frac{3}{2}}\)的定义域和值域。
解析:
\(y=x^{\frac{3}{2}}=\sqrt{x^3}\),偶数次根号下\(x^3\geq0\),即\(x\geq0\),定义域为\([0,+\infty)\);当\(x\geq0\)时,\(\sqrt{x^3}\geq0\),值域为\([0,+\infty)\)。
答案:定义域\([0,+\infty)\),值域\([0,+\infty)\)。
例题3:求幂函数\(y=x^{-\frac{2}{3}}\)的定义域和值域。
解析:
\(y=x^{-\frac{2}{3}}=\frac{1}{\sqrt[3]{x^2}}\),三次根号下全体实数有意义,且分母不为0,定义域为\(x\neq0\)(即\((-\infty,0)\cup(0,+\infty)\));\(x^2>0\),则\(\sqrt[3]{x^2}>0\),值域为\((0,+\infty)\)。
答案:定义域\((-\infty,0)\cup(0,+\infty)\),值域\((0,+\infty)\)。
例题4:已知幂函数\(f(x)=x^a\)的图像过点\((4,2)\),求\(a\)的值和\(f(9)\)。
解析:
代入点\((4,2)\)得\(4^a=2\),即\((2^2)^a=2^1\),所以\(2a=1\),\(a=\frac{1}{2}\);则\(f(x)=x^{\frac{1}{2}}=\sqrt{x}\),\(f(9)=\sqrt{9}=3\)。
答案:\(a=\frac{1}{2}\),\(f(9)=3\)。
例题5:若幂函数\(y=x^a\)的定义域为\(\mathbb{R}\),则\(a\)的取值范围是什么?
解析:
定义域为\(\mathbb{R}\)需满足“任何实数\(x\)代入都有意义”。当\(a\)为正整数(如\(1,2\))、\(a\)为正分数且分母为奇数(如\(\frac{1}{3},\frac{2}{3}\))时,定义域为\(\mathbb{R}\);若\(a\)为负整数或分母为偶数的分数,定义域会排除0或负数,不满足。
答案:\(a\)为正整数,或\(a\)为正分数且分母为奇数(\(a=\frac{p}{q}\),\(p,q\)正整数互质,\(q\)奇)。
例题6:判断幂函数\(y=x^3\)的单调性和奇偶性。
解析:
单调性:任取\(x_1<x_2\),\(x_1^3 - x_2^3=(x_1 - x_2)(x_1^2 + x_1x_2 + x_2^2)<0\)(因\(x_1 - x_2<0\),后面式子恒正),故在\(\mathbb{R}\)上单调递增;奇偶性:定义域\(\mathbb{R}\)关于原点对称,且\(f(-x)=(-x)^3=-x^3=-f(x)\),是奇函数。
答案:在\(\mathbb{R}\)上单调递增,是奇函数。
例题7:判断幂函数\(y=x^{-2}\)在\((0,+\infty)\)上的单调性。
解析:
任取\(0<x_1<x_2\),\(f(x_1)-f(x_2)=\frac{1}{x_1^2}-\frac{1}{x_2^2}=\frac{x_2^2 - x_1^2}{x_1^2x_2^2}=\frac{(x_2 - x_1)(x_2 + x_1)}{x_1^2x_2^2}>0\)(因\(x_2 - x_1>0\),其余项均正),故在\((0,+\infty)\)上单调递减。
答案:在\((0,+\infty)\)上单调递减。
例题8:比较大小:①\(2.1^{\frac{1}{2}}\)与\(1.9^{\frac{1}{2}}\);②\((-0.8)^3\)与\((-0.7)^3\)。
解析:
①\(y=x^{\frac{1}{2}}=\sqrt{x}\)在\([0,+\infty)\)上单调递增,\(2.1>1.9\),故\(2.1^{\frac{1}{2}}>1.9^{\frac{1}{2}}\);②\(y=x^3\)在\(\mathbb{R}\)上单调递增,\(-0.8<-0.7\),故\((-0.8)^3<(-0.7)^3\)。
答案:①\(2.1^{\frac{1}{2}}>1.9^{\frac{1}{2}}\);②\((-0.8)^3<(-0.7)^3\)。
例题9:比较大小:①\(0.3^{-2}\)与\(0.4^{-2}\);②\(1.2^{-\frac{1}{3}}\)与\(1.3^{-\frac{1}{3}}\)。
解析:
①\(y=x^{-2}=\frac{1}{x^2}\)在\((0,+\infty)\)上单调递减,\(0.3<0.4\),故\(0.3^{-2}>0.4^{-2}\);②\(y=x^{-\frac{1}{3}}=\frac{1}{\sqrt[3]{x}}\)在\((0,+\infty)\)上单调递减,\(1.2<1.3\),故\(1.2^{-\frac{1}{3}}>1.3^{-\frac{1}{3}}\)。
答案:①\(0.3^{-2}>0.4^{-2}\);②\(1.2^{-\frac{1}{3}}>1.3^{-\frac{1}{3}}\)。
例题10:已知幂函数\(f(x)=x^a\)是偶函数,且在\((0,+\infty)\)上单调递减,求\(a\)的一个可能值。
解析:
偶函数需满足“\(a\)为偶数或分子为偶的分数(分母奇)”,在\((0,+\infty)\)递减需满足“\(a<0\)”,故\(a\)可为\(-2,-4,-\frac{2}{3}\)等。
答案:\(a=-2\)(答案不唯一)。
例题11:判断幂函数\(y=x^{\frac{1}{3}}\)的奇偶性,并证明\(f(-x)=-f(x)\)。
解析:
定义域为\(\mathbb{R}\),关于原点对称;\(f(-x)=(-x)^{\frac{1}{3}}=\sqrt[3]{-x}=-\sqrt[3]{x}=-x^{\frac{1}{3}}=-f(x)\),故为奇函数。
答案:是奇函数,证明如上。
例题12:已知幂函数\(f(x)\)在\((0,+\infty)\)上单调递增,且\(f(2)>f(1.5)\),则\(f(x)\)的指数\(a\)满足什么条件?
解析:
幂函数在\((0,+\infty)\)上单调递增的充要条件是\(a>0\),而\(f(2)>f(1.5)\)正是递增的体现,故只需\(a>0\)。
答案:\(a>0\)。
例题13:求幂函数\(y=x^{\frac{2}{3}}\)在区间\([-8,8]\)上的最大值和最小值。
解析:
\(y=x^{\frac{2}{3}}=\sqrt[3]{x^2}\),是偶函数,且在\([0,8]\)上单调递增(因\(a=\frac{2}{3}>0\),分母奇);在\([0,8]\)上,最大值为\(8^{\frac{2}{3}}=(\sqrt[3]{8})^2=2^2=4\),最小值为\(0^{\frac{2}{3}}=0\);因是偶函数,\([-8,0]\)上最大值也为4,最小值为0,故整个区间最大值4,最小值0。
答案:最大值4,最小值0。
例题14:判断幂函数\(y=x^{-\frac{1}{2}}\)是否为奇函数,并说明理由。
解析:
定义域为\(x>0\),不关于原点对称(若取\(x=1\),则\(-1\)不在定义域内),不满足奇偶性的前提条件,故非奇非偶。
答案:非奇非偶,理由是定义域不关于原点对称。
例题15:已知\(a>0\)且\(a\neq1\),比较\(a^{0.5}\)与\(a^{0.3}\)的大小,若将“\(a\)”换成幂函数\(y=x^{0.5}\)与\(y=x^{0.3}\),比较\(2^{0.5}\)与\(2^{0.3}\)的大小,两者有何区别?
解析:
前者是指数函数\(y=a^x\),单调性由\(a\)决定(\(a>1\)时递增,\(0<a<1\)时递减),无法直接比较;后者是幂函数,\(y=x^a\)(\(a>0\))在\((0,+\infty)\)上递增,\(0.5>0.3\),故\(2^{0.5}>2^{0.3}\);区别:指数函数自变量在指数,单调性由底数决定;幂函数自变量在底数,单调性由指数决定。
答案:指数函数需分\(a>1\)和\(0<a<1\),幂函数中\(2^{0.5}>2^{0.3}\);区别如上。
例题16:幂函数\(y=x^a\)的图像过点\((2,8)\),且与直线\(y=x\)交于点\(P\),求点\(P\)的坐标。
解析:
代入\((2,8)\)得\(2^a=8=2^3\),故\(a=3\),幂函数为\(y=x^3\);联立\(y=x^3\)与\(y=x\),得\(x^3=x\),即\(x(x^2 - 1)=0\),解得\(x=0,1,-1\),对应\(y=0,1,-1\),故点\(P\)为\((0,0),(1,1),(-1,-1)\)。
答案:\((0,0),(1,1),(-1,-1)\)。
例题17:解不等式\((x-1)^{\frac{1}{2}} < (3-2x)^{\frac{1}{2}}\)。
解析:
幂函数\(y=x^{\frac{1}{2}}=\sqrt{x}\)的定义域为\(x\geq0\),且在\([0,+\infty)\)上单调递增,故不等式等价于:\(\begin{cases}x-1\geq0 \\ 3-2x\geq0 \\ x-1 < 3-2x\end{cases}\);解第一个不等式得\(x\geq1\),第二个得\(x\leq\frac{3}{2}\),第三个得\(x<\frac{4}{3}\),综上\(1\leq x\leq\frac{3}{2}\)。
答案:\([1,\frac{3}{2}]\)。
例题18:解不等式\((x+2)^{-3} > (1-2x)^{-3}\)。
解析:
幂函数\(y=x^{-3}=\frac{1}{x^3}\)的定义域为\(x\neq0\),且在\((-\infty,0)\)和\((0,+\infty)\)上分别单调递减,故分情况讨论:
① 当\(x+2>0\)且\(1-2x>0\)(即\(-2<x<\frac{1}{2}\))时,因在\((0,+\infty)\)递减,不等式等价于\(x+2 < 1-2x\),解得\(x<-\frac{1}{3}\),结合范围得\(-2<x<-\frac{1}{3}\);
② 当\(x+2<0\)且\(1-2x<0\)(即\(x<-2\)且\(x>\frac{1}{2}\))时,无交集,无解;
③ 当\(x+2>0\)且\(1-2x<0\)(即\(x>\frac{1}{2}\))时,左边正、右边负,不等式恒成立;
④ 当\(x+2<0\)且\(1-2x>0\)(即\(x<-2\))时,左边负、右边正,不等式不成立;
综上,解集为\((-2,-\frac{1}{3})\cup(\frac{1}{2},+\infty)\)。
答案:\((-2,-\frac{1}{3})\cup(\frac{1}{2},+\infty)\)。
例题19:已知幂函数\(f(x)=(m^2 - m - 1)x^{m^2 - 2m - 3}\),当\(x\in(0,+\infty)\)时\(f(x)\)单调递减,求\(m\)的值。
解析:
首先,幂函数的系数必须为1,故\(m^2 - m - 1=1\),解得\(m^2 - m - 2=0\),即\(m=2\)或\(m=-1\);
其次,当\(x\in(0,+\infty)\)时单调递减,需指数\(m^2 - 2m - 3<0\);
当\(m=2\)时,指数为\(4 - 4 - 3=-3<0\),满足条件;
当\(m=-1\)时,指数为\(1 + 2 - 3=0\),此时\(f(x)=x^0=1\)(\(x\neq0\)),是常函数,不单调递减,舍去;
故\(m=2\)。
答案:\(m=2\)。
例题20:已知幂函数\(y=x^a\)和\(y=x^b\)的图像分别过点\((2,\sqrt{2})\)和\((\sqrt{3},3)\),比较\(a\)和\(b\)的大小。
解析:
对\(y=x^a\),代入\((2,\sqrt{2})\)得\(2^a=2^{\frac{1}{2}}\),故\(a=\frac{1}{2}\);对\(y=x^b\),代入\((\sqrt{3},3)\)得\((3^{\frac{1}{2}})^b=3^1\),即\(3^{\frac{b}{2}}=3^1\),故\(\frac{b}{2}=1\),\(b=2\);因此\(a=\frac{1}{2}<b=2\)。
答案:\(a<b\)。
数学基础 : 小学数学、初中数学、高中数学、高等数学
- 函数的恒成立、存在性问题
- 不等式的缩放
- 基于函数单调性的不等式缩放
- 基于函数凹凸性的不等式缩放
- 函数同构问题:形式统一,单调性搭桥
- 映射、函数:\( f: A \to B \)
- 函数的定义域:Df
- 函数的值域:Rf
- 函数的解析式:f(x)
- 抽象函数:定义域、值域、解析式
- 分段函数:定义域、值域、单调性
- 复合函数: y = f[g(x)]
- 反函数:严格单调函数
- 隐函数:F(x, y) = 0
- 函数的有界性:\( |f(x)| \leq M \)
- 函数的单调性:增函数、减函数
- 函数的奇偶性:奇函数、偶函数
- 函数的周期性:\( f(x + T) = f(x) \)
- 类周期性:\(f(x+T)=f(x)+g(x)\)
- 函数的对称性:自对称、互对称
- 函数的凹凸性:凹函数、凸函数
- 图象平移、对称、翻折、缩放、旋转
- 函数的极值、函数的最值
- 二次函数:最值、根的分布、恒成立问题
- 三次函数:\( f(x) = ax^3 + bx^2 + cx + d \)
- 幂函数: \(y = x^a\)
- 对勾函数与双刀函数
- 指数方程:\(a^{x}=b\)(\(a > 0\)且\(a\neq1\))
- 指数函数:\(y = a^{x}(a>0\),且\(a\neq1)\)
- 双曲函数与反双曲函数
- 对数函数:对数运算性质
- 导数同构与导数异构
- 角度制与弧度制、弧长公式
- 三角函数:定义、性质
- 三角函数:诱导公式、恒等变换、辅助角
- 反三角函数:\(\arcsin x\)
- 三角函数二级结论
- 三角形内角的三角函数
- 数学中各类角的范围速记表
- 极坐标:\((\rho,\theta)\)=(极径,极角)
- 参数方程
- 等差数列
- 等比数列
- 数学归纳法
- 求和符号(∑ )、连乘符号(∏)
- 数列极限、函数极限
- 函数的连续性:间断点、运算法则
- 函数的导数
- 函数的图形
- 函数的微分
