对数函数：对数运算性质

陈一男学习网站[ ChenYinan.com ] - 中国数学学会 - 中国院士 - GeoGebra - 数学基础

一、对数的定义

如果 \( a^x = N \)（其中 \( a > 0 \) 且 \( a \neq 1 \)，\( N > 0 \)），那么数 \( x \) 叫做以 \( a \) 为底 \( N \) 的对数，记作 \( x = \log_a N \)。

核心要素：底数 \( a \) 满足 \( a > 0 \) 且 \( a \neq 1 \)，真数 \( N \) 必须大于 0（对数的定义域要求）。

特殊对数：常用对数 \( \lg N = \log_{10} N \)，自然对数 \( \ln N = \log_e N \)（\( e \approx 2.71828 \)）。

指数与对数的互化：\( a^x = N \iff x = \log_a N \)，这是对数运算的基础。

二、对数的性质

零和负数没有对数，即 \( N \leq 0 \) 时，\( \log_a N \) 无意义。

底数的对数等于 1：\( \log_a a = 1 \)（因为 \( a^1 = a \)）。

1 的对数等于 0：\( \log_a 1 = 0 \)（因为 \( a^0 = 1 \)）。

对数恒等式：\( a^{\log_a N} = N \)（将对数式代回指数式直接可得）。

换底公式：\( \log_a N = \frac{\log_b N}{\log_b a} \)（\( b > 0 \) 且 \( b \neq 1 \)），可将不同底数的对数转化为同底数对数计算。

三、对数的运算法则（\( a > 0 \) 且 \( a \neq 1 \)，\( M > 0 \)，\( N > 0 \)）

积的对数：\( \log_a (M \cdot N) = \log_a M + \log_a N \)（对数将乘法转化为加法）。

商的对数：\( \log_a \frac{M}{N} = \log_a M - \log_a N \)（对数将除法转化为减法）。

幂的对数：\( \log_a M^k = k \log_a M \)（\( k \) 为任意实数，可将指数提到对数前）。

根的对数：\( \log_a \sqrt[k]{M} = \frac{1}{k} \log_a M \)（本质是幂的对数的推论，\( \sqrt[k]{M} = M^{\frac{1}{k}} \)）。

四、对数的二级结论（常用推论）

换底公式推论 1：\( \log_a b \cdot \log_b a = 1 \)（由换底公式可得 \( \frac{\ln b}{\ln a} \cdot \frac{\ln a}{\ln b} = 1 \)）。

换底公式推论 2：\( \log_{a^m} b^n = \frac{n}{m} \log_a b \)（通过换底公式转化后化简）。

连锁对数：\( \log_a b \cdot \log_b c \cdot \log_c a = 1 \)（多次应用换底公式约分可得）。

对数恒等变形：\( \log_a (M^n \cdot N^m) = n \log_a M + m \log_a N \)（结合积的对数和幂的对数法则）。

倒数关系：\( \log_a \frac{1}{N} = -\log_a N \)（由商的对数 \( \log_a 1 - \log_a N = 0 - \log_a N \) 推导）。

底数幂与对数：\( \log_{a^k} N = \frac{1}{k} \log_a N \)（幂的对数法则的反向应用）。

五、对数函数

1. 定义

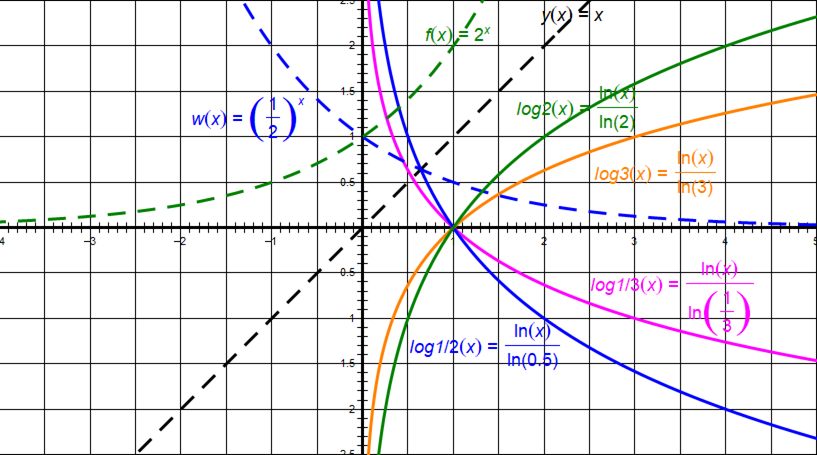
函数 \( y = \log_a x \)（其中 \( a > 0 \) 且 \( a \neq 1 \)，定义域 \( x > 0 \)，值域 \( \mathbb{R} \)）叫做对数函数，是指数函数 \( y = a^x \) 的反函数。

2. 图像与性质（分底数 \( a > 1 \) 和 \( 0 < a < 1 \) 两种情况）

共性：图像都过定点 \( (1, 0) \)；定义域均为 \( (0, +\infty) \)；值域均为 \( \mathbb{R} \)；图像在 \( y \) 轴右侧。

当 \( a > 1 \) 时：函数在 \( (0, +\infty) \) 上单调递增；当 \( x > 1 \) 时，\( y > 0 \)；当 \( 0 < x < 1 \) 时，\( y < 0 \)。

当 \( 0 < a < 1 \) 时：函数在 \( (0, +\infty) \) 上单调递减；当 \( x > 1 \) 时，\( y < 0 \)；当 \( 0 < x < 1 \) 时，\( y > 0 \)。

3. 单调性应用

比较对数大小：若底数相同，利用单调性；若底数不同，用换底公式转化为同底数或找中间量（如 0、1）。

解对数不等式：先保证真数大于 0，再根据底数的单调性去掉对数符号，注意不等号方向的变化。

对数函数的图象

例题 1：指数与对数互化：将 \( 2^5 = 32 \) 化为对数式，\( \log_3 81 = 4 \) 化为指数式。

解析：

由互化关系 \( a^x = N \iff x = \log_a N \)，得 \( \log_2 32 = 5 \)；\( 3^4 = 81 \)。

例题 2：求对数的值（基础）计算 \( \log_5 25 \)、\( \lg 1000 \)、\( \ln e^2 \)。

解析：

\( \log_5 25 = \log_5 5^2 = 2 \)；\( \lg 1000 = \log_{10} 10^3 = 3 \)；\( \ln e^2 = 2 \ln e = 2 \)。

例题 3：利用对数恒等式计算：计算 \( 3^{\log_3 7} \)、\( 10^{\lg 0.5} \)。

解析：

由 \( a^{\log_a N} = N \)，得 \( 3^{\log_3 7} = 7 \)；\( 10^{\lg 0.5} = 0.5 \)。

例题 4：换底公式的应用：计算 \( \log_4 8 \)、\( \log_2 5 \cdot \log_5 8 \)。

解析：

\( \log_4 8 = \frac{\log_2 8}{\log_2 4} = \frac{3}{2} \)；\( \log_2 5 \cdot \log_5 8 = \frac{\ln 5}{\ln 2} \cdot \frac{\ln 8}{\ln 5} = \log_2 8 = 3 \)。

例题 5：对数运算法则（积的对数）计算 \( \log_2 (4 \times 8) \)、\( \lg 2 + \lg 5 \)。

解析：

\( \log_2 (4 \times 8) = \log_2 4 + \log_2 8 = 2 + 3 = 5 \)；\( \lg 2 + \lg 5 = \lg (2 \times 5) = \lg 10 = 1 \)。

例题 6：对数运算法则（商的对数）计算 \( \log_3 \frac{81}{27} \)、\( \ln e^3 - \ln e \)。

解析：

\( \log_3 \frac{81}{27} = \log_3 81 - \log_3 27 = 4 - 3 = 1 \)；\( \ln e^3 - \ln e = \ln \frac{e^3}{e} = \ln e^2 = 2 \)。

例题 7：对数运算法则（幂的对数）计算 \( \log_2 8^4 \)、\( \lg \sqrt{1000} \)。

解析：

\( \log_2 8^4 = 4 \log_2 8 = 4 \times 3 = 12 \)；\( \lg \sqrt{1000} = \lg 10^{\frac{3}{2}} = \frac{3}{2} \)。

例题 8：混合运算法则应用：计算 \( \log_a (a^2 \cdot \sqrt{a}) \)（\( a > 0 \) 且 \( a \neq 1 \)）。

解析：

原式 \( = \log_a a^2 + \log_a a^{\frac{1}{2}} = 2 + \frac{1}{2} = \frac{5}{2} \)。

例题 9：二级结论（\( \log_a b \cdot \log_b a = 1 \)）计算 \( \log_{12} 6 \cdot \log_6 12 \)、\( \log_5 3 \cdot \log_3 5 \cdot \log_2 4 \)。

解析：

第一式直接用结论得 1；第二式 \( = 1 \times \log_2 2^2 = 2 \)。

例题 10：二级结论（\( \log_{a^m} b^n = \frac{n}{m} \log_a b \)）计算 \( \log_{2^3} 3^2 \)、\( \log_{9} 27 \)。

解析：

\( \log_{2^3} 3^2 = \frac{2}{3} \log_2 3 \)；\( \log_9 27 = \log_{3^2} 3^3 = \frac{3}{2} \log_3 3 = \frac{3}{2} \)。

例题 11：对数函数定义域求解：求函数 \( y = \log_2 (3x - 1) \)、\( y = \lg \frac{1}{1 - x} \) 的定义域。

解析：

第一式需 \( 3x - 1 > 0 \implies x > \frac{1}{3} \)，定义域为 \( (\frac{1}{3}, +\infty) \)；第二式需 \( \frac{1}{1 - x} > 0 \implies 1 - x > 0 \implies x < 1 \)，定义域为 \( (-\infty, 1) \)。

例题 12：对数函数过定点问题：求函数 \( y = \log_3 (x - 2) + 1 \) 过的定点。

解析：

令 \( x - 2 = 1 \implies x = 3 \)，此时 \( y = 0 + 1 = 1 \)，定点为 \( (3, 1) \)。

例题 13：对数函数单调性比较大小：比较下列各组大小：（1）\( \log_2 5 \) 与 \( \log_2 3 \)；（2）\( \log_{0.5} 4 \) 与 \( \log_{0.5} 6 \)。

解析：

（1）\( a = 2 > 1 \)，函数单调递增，\( 5 > 3 \implies \log_2 5 > \log_2 3 \)；（2）\( 0 < a = 0.5 < 1 \)，函数单调递减，\( 4 < 6 \implies \log_{0.5} 4 > \log_{0.5} 6 \)。

例题 14：不同底数对数比较大小：比较 \( \log_3 4 \) 与 \( \log_4 5 \)。

解析：

用换底公式转化为自然对数，\( \log_3 4 = \frac{\ln 4}{\ln 3} \)，\( \log_4 5 = \frac{\ln 5}{\ln 4} \)，作差 \( \frac{\ln^2 4 - \ln 3 \ln 5}{\ln 3 \ln 4} \)，由均值不等式 \( \ln 3 \ln 5 < (\frac{\ln 3 + \ln 5}{2})^2 = (\frac{\ln 15}{2})^2 < (\frac{\ln 16}{2})^2 = (\ln 4)^2 \)，故 \( \log_3 4 > \log_4 5 \)。

例题 15：解对数方程（基础）解方程 \( \log_2 (x + 1) = 3 \)、\( \lg x^2 = 2 \)。

解析：

第一式 \( x + 1 = 2^3 = 8 \implies x = 7 \)（验证真数大于 0，成立）；第二式 \( x^2 = 10^2 = 100 \implies x = \pm 10 \)（验证 \( x = \pm 10 \) 时 \( x^2 > 0 \)，均成立）。

例题 16：解对数方程（含运算法则）解方程 \( \log_3 (x - 2) + \log_3 (x + 1) = 1 \)。

解析：

先合并对数，\( \log_3 [(x - 2)(x + 1)] = 1 \implies (x - 2)(x + 1) = 3^1 = 3 \)，整理得 \( x^2 - x - 5 = 0 \)，解得 \( x = \frac{1 \pm \sqrt{21}}{2} \)，验证真数：\( x > 2 \)，故 \( x = \frac{1 + \sqrt{21}}{2} \)。

例题 17：解对数不等式（基础）解不等式 \( \log_2 (2x - 1) > 1 \)、\( \log_{0.3} (x + 3) > 0 \)。

解析：

第一式 \( 2x - 1 > 2^1 = 2 \implies x > \frac{3}{2} \)；第二式 \( 0 < x + 3 < 0.3^0 = 1 \implies -3 < x < -2 \)。

例题 18：解对数不等式（含参数）解不等式 \( \log_a (x - 1) > \log_a (2x - 3) \)（\( a > 0 \) 且 \( a \neq 1 \)）。

解析：

当 \( a > 1 \) 时，函数单调递增，需 \( x - 1 > 2x - 3 > 0 \implies \frac{3}{2} < x < 2 \)；当 \( 0 < a < 1 \) 时，函数单调递减，需 \( 0 < x - 1 < 2x - 3 \implies x > 2 \)。

例题 19：对数函数值域求解：求函数 \( y = \log_2 (x^2 + 1) \)、\( y = \log_{0.5} (4 - x^2) \) 的值域。

解析：

第一式 \( x^2 + 1 \geq 1 \)，\( a = 2 > 1 \)，故值域为 \( [0, +\infty) \)；第二式 \( 0 < 4 - x^2 \leq 4 \)，\( 0 < a = 0.5 < 1 \)，故值域为 \( [-2, +\infty) \)。

例题 20：对数函数综合应用（实际问题）某城市人口年增长率为 \( 10\% \)，多少年后人口达到原来的 2 倍？（结果保留整数，\( \lg 2 \approx 0.3010 \)，\( \lg 1.1 \approx 0.0414 \)）

解析：

设初始人口为 \( P \)，\( n \) 年后人口为 \( 2P \)，则 \( P(1 + 10\%)^n = 2P \implies 1.1^n = 2 \)，取常用对数 \( n \lg 1.1 = \lg 2 \implies n = \frac{\lg 2}{\lg 1.1} \approx \frac{0.3010}{0.0414} \approx 7 \)，故约 7 年后人口达到原来的 2 倍。