双曲函数与反双曲函数
双曲函数是一类与三角函数形式相似,但基于指数函数定义的初等函数,广泛应用于工程力学(如悬链线)、热力学、概率论等领域;反双曲函数则是双曲函数的逆运算,用于解决“已知双曲函数值求自变量”的问题。
一、双曲函数的定义(基于指数函数)
双曲函数共6个,核心是双曲正弦(sinh) 和双曲余弦(cosh),其余4个由二者推导而来,定义如下(定义域均为 \( \mathbb{R} \)):
双曲正弦:\( \sinh x = \frac{e^x - e^{-x}}{2} \)(“sinh”读作“sin h”,h为“hyperbolic”缩写);
双曲余弦:\( \cosh x = \frac{e^x + e^{-x}}{2} \)(“cosh”读作“cos h”);
双曲正切:\( \tanh x = \frac{\sinh x}{\cosh x} = \frac{e^x - e^{-x}}{e^x + e^{-x}} \)(“tanh”读作“tan h”);
双曲余切:\( \coth x = \frac{\cosh x}{\sinh x} = \frac{e^x + e^{-x}}{e^x - e^{-x}} \)(定义域:\( x \neq 0 \),“coth”读作“cot h”);
双曲正割:\( \text{sech } x = \frac{1}{\cosh x} = \frac{2}{e^x + e^{-x}} \)(“sech”读作“sec h”);
双曲余割:\( \text{csch } x = \frac{1}{\sinh x} = \frac{2}{e^x - e^{-x}} \)(定义域:\( x \neq 0 \),“csch”读作“csc h”)。
二、双曲函数的性质(与三角函数对比)
双曲函数的性质与三角函数既有相似性(如奇偶性、恒等式),也有本质差异(如单调性、有界性),核心性质如下:
1、奇偶性
奇函数:\( \sinh(-x) = -\sinh x \)、\( \tanh(-x) = -\tanh x \)、\( \text{csch}(-x) = -\text{csch} x \)(与 \( \sin x, \tan x, \csc x \) 一致);
偶函数:\( \cosh(-x) = \cosh x \)、\( \text{sech}(-x) = \text{sech} x \)(与 \( \cos x, \sec x \) 一致);
非奇非偶:\( \coth(-x) = -\coth x \)(实际为奇函数,因 \( \coth x = \frac{1}{\tanh x} \),奇函数的倒数仍为奇函数)。
2、核心恒等式(高频使用)
平方关系:\( \cosh^2 x - \sinh^2 x = 1 \)(类比 \( \cos^2 x + \sin^2 x = 1 \),注意符号差异);
推导:\( \cosh^2 x - \sinh^2 x = \left( \frac{e^x + e^{-x}}{2} \right)^2 - \left( \frac{e^x - e^{-x}}{2} \right)^2 = \frac{e^{2x} + 2 + e^{-2x} - (e^{2x} - 2 + e^{-2x})}{4} = 1 \);
正切平方关系:\( 1 - \tanh^2 x = \text{sech}^2 x \)(由平方关系两边除以 \( \cosh^2 x \) 得);
余切平方关系:\( \coth^2 x - 1 = \text{csch}^2 x \)(由平方关系两边除以 \( \sinh^2 x \) 得);
和角公式:\( \sinh(x \pm y) = \sinh x \cosh y \pm \cosh x \sinh y \)、\( \cosh(x \pm y) = \cosh x \cosh y \pm \sinh x \sinh y \)(与三角函数和角公式类似,符号一致)。
3、单调性与有界性
单调递增:\( \sinh x \)(值域 \( \mathbb{R} \))、\( \tanh x \)(值域 \( (-1, 1) \),有界);
分段单调:\( \cosh x \)(在 \( (-\infty, 0] \) 单调递减,在 \( [0, +\infty) \) 单调递增,最小值为 \( \cosh 0 = 1 \),值域 \( [1, +\infty) \));
有界函数:仅 \( \tanh x \)(\( |\tanh x| < 1 \))和 \( \text{sech} x \)(\( 0 < \text{sech} x \leq 1 \)),其余双曲函数均无界。
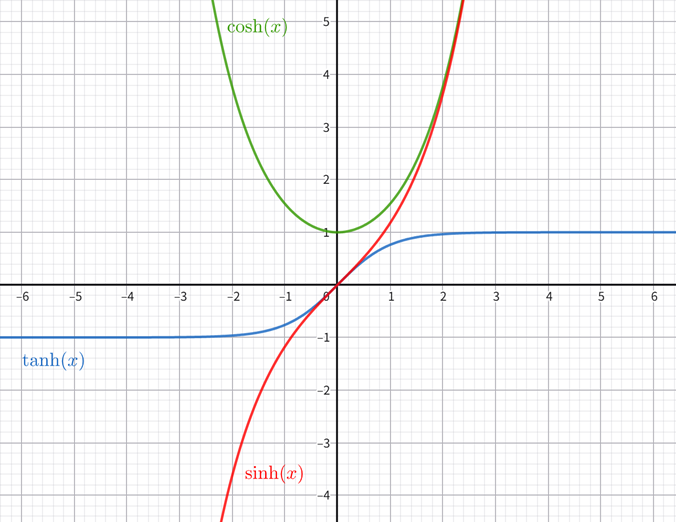
三、双曲函数的图像特征(辅助理解)
\( \sinh x \):过原点,类似三次函数,在 \( \mathbb{R} \) 上单调递增,当 \( x \to +\infty \) 时,\( \sinh x \approx \frac{e^x}{2} \);当 \( x \to -\infty \) 时,\( \sinh x \approx -\frac{e^{-x}}{2} \);
\( \cosh x \):过点 \( (0,1) \),图像为“悬链线”,在 \( x=0 \) 处取得最小值1,当 \( x \to \pm\infty \) 时,\( \cosh x \approx \frac{e^{|x|}}{2} \);
\( \tanh x \):过原点,在 \( \mathbb{R} \) 上单调递增,水平渐近线为 \( y=1 \)(\( x \to +\infty \))和 \( y=-1 \)(\( x \to -\infty \))。
四、反双曲函数的定义(双曲函数的逆运算)
双曲函数中,\( \sinh x \)(严格递增)、\( \tanh x \)(严格递增)、\( \text{sech} x \)(在 \( [0, +\infty) \) 严格递减)、\( \cosh x \)(在 \( [0, +\infty) \) 严格递增)存在逆函数,称为反双曲函数,定义如下(均通过“解方程法”推导,即令 \( y = \text{双曲函数}(x) \),解出 \( x \) 作为 \( y \) 的函数):
反双曲正弦:\( \text{arsinh } x = \ln(x + \sqrt{x^2 + 1}) \)(定义域 \( \mathbb{R} \),“arsinh”读作“arc sin h”);
反双曲余弦:\( \text{arcosh } x = \ln(x + \sqrt{x^2 - 1}) \)(定义域 \( [1, +\infty) \),因 \( \cosh x \) 的值域为 \( [1, +\infty) \),且取 \( \cosh x \) 在 \( [0, +\infty) \) 的逆,故值域 \( [0, +\infty) \));
反双曲正切:\( \text{artanh } x = \frac{1}{2}\ln\left( \frac{1 + x}{1 - x} \right) \)(定义域 \( (-1, 1) \),因 \( \tanh x \) 的值域为 \( (-1, 1) \));
反双曲余切:\( \text{arcoth } x = \frac{1}{2}\ln\left( \frac{x + 1}{x - 1} \right) \)(定义域 \( (-\infty, -1) \cup (1, +\infty) \),因 \( \coth x \) 的值域为 \( (-\infty, -1) \cup (1, +\infty) \));
反双曲正割:\( \text{arsech } x = \ln\left( \frac{1 + \sqrt{1 - x^2}}{x} \right) \)(定义域 \( (0, 1] \),因 \( \text{sech} x \) 的值域为 \( (0, 1] \));
反双曲余割:\( \text{arcsch } x = \ln\left( \frac{1}{x} + \sqrt{\frac{1}{x^2} + 1} \right) \)(定义域 \( \mathbb{R} \setminus \{0\} \),因 \( \text{csch} x \) 的值域为 \( \mathbb{R} \setminus \{0\} \))。
五、反双曲函数的性质
奇偶性:\( \text{arsinh}(-x) = -\text{arsinh} x \)(奇函数)、\( \text{arcoth}(-x) = -\text{arcoth} x \)(奇函数)、\( \text{arcsch}(-x) = -\text{arcsch} x \)(奇函数);\( \text{arcosh} x \)、\( \text{arsech} x \) 非奇非偶(因定义域不对称);
单调性:\( \text{arsinh} x \)(\( \mathbb{R} \) 上严格递增)、\( \text{arcosh} x \)(\( [1, +\infty) \) 上严格递增)、\( \text{artanh} x \)(\( (-1, 1) \) 上严格递增);
与对数函数的关系:所有反双曲函数均可表示为自然对数的形式(定义已体现),这是其与反三角函数的核心差异(反三角函数无法用初等函数显式表示)。
例题1:求 \( \sinh 0 \)、\( \cosh 0 \)、\( \tanh 0 \) 的值
分析:代入双曲函数定义:
\( \sinh 0 = \frac{e^0 - e^{-0}}{2} = \frac{1 - 1}{2} = 0 \);
\( \cosh 0 = \frac{e^0 + e^{-0}}{2} = \frac{1 + 1}{2} = 1 \);
\( \tanh 0 = \frac{\sinh 0}{\cosh 0} = \frac{0}{1} = 0 \)。
结论:\( \sinh 0 = 0 \),\( \cosh 0 = 1 \),\( \tanh 0 = 0 \)。
例题2:求 \( \sinh(\ln 2) \) 和 \( \cosh(\ln 2) \) 的值
分析:利用指数函数与对数函数的关系 \( e^{\ln a} = a \)、\( e^{-\ln a} = \frac{1}{a} \):
\( \sinh(\ln 2) = \frac{e^{\ln 2} - e^{-\ln 2}}{2} = \frac{2 - \frac{1}{2}}{2} = \frac{\frac{3}{2}}{2} = \frac{3}{4} \);
\( \cosh(\ln 2) = \frac{e^{\ln 2} + e^{-\ln 2}}{2} = \frac{2 + \frac{1}{2}}{2} = \frac{\frac{5}{2}}{2} = \frac{5}{4} \)。
结论:\( \sinh(\ln 2) = \frac{3}{4} \),\( \cosh(\ln 2) = \frac{5}{4} \)。
例题3:证明恒等式 \( \cosh 2x = \cosh^2 x + \sinh^2 x \)
分析:利用双曲函数定义展开右边,化简后与左边对比:
右边:\( \cosh^2 x + \sinh^2 x = \left( \frac{e^x + e^{-x}}{2} \right)^2 + \left( \frac{e^x - e^{-x}}{2} \right)^2 \);
展开:\( \frac{e^{2x} + 2 + e^{-2x}}{4} + \frac{e^{2x} - 2 + e^{-2x}}{4} = \frac{2e^{2x} + 2e^{-2x}}{4} = \frac{e^{2x} + e^{-2x}}{2} \);
左边:\( \cosh 2x = \frac{e^{2x} + e^{-2x}}{2} \)(代入双曲余弦定义,将 \( x \) 替换为 \( 2x \))。
结论:右边=左边,恒等式成立。
例题4:证明恒等式 \( \sinh 2x = 2\sinh x \cosh x \)
分析:展开右边,化简后与左边对比:
右边:\( 2\sinh x \cosh x = 2 \cdot \frac{e^x - e^{-x}}{2} \cdot \frac{e^x + e^{-x}}{2} = 2 \cdot \frac{e^{2x} - e^{-2x}}{4} = \frac{e^{2x} - e^{-2x}}{2} \);
左边:\( \sinh 2x = \frac{e^{2x} - e^{-2x}}{2} \)(双曲正弦定义,\( x \) 替换为 \( 2x \))。
结论:右边=左边,恒等式成立。
例题5:已知 \( \sinh x = 3 \),求 \( \cosh x \) 和 \( \tanh x \) 的值
分析:利用平方关系 \( \cosh^2 x - \sinh^2 x = 1 \):
由 \( \cosh^2 x = \sinh^2 x + 1 = 3^2 + 1 = 10 \),因 \( \cosh x \geq 1 \)(值域特性),故 \( \cosh x = \sqrt{10} \)(舍去负根);
\( \tanh x = \frac{\sinh x}{\cosh x} = \frac{3}{\sqrt{10}} = \frac{3\sqrt{10}}{10} \)。
结论:\( \cosh x = \sqrt{10} \),\( \tanh x = \frac{3\sqrt{10}}{10} \)。
例题6:已知 \( \cosh x = \frac{5}{3} \),求 \( \sinh x \) 和 \( \coth x \) 的值(\( x > 0 \))
分析:利用平方关系,结合 \( x > 0 \) 确定 \( \sinh x \) 符号:
\( \sinh^2 x = \cosh^2 x - 1 = \left( \frac{5}{3} \right)^2 - 1 = \frac{25}{9} - 1 = \frac{16}{9} \),因 \( x > 0 \) 时 \( \sinh x > 0 \),故 \( \sinh x = \frac{4}{3} \);
\( \coth x = \frac{\cosh x}{\sinh x} = \frac{\frac{5}{3}}{\frac{4}{3}} = \frac{5}{4} \)。
结论:\( \sinh x = \frac{4}{3} \),\( \coth x = \frac{5}{4} \)。
例题7:求函数 \( f(x) = \sinh(2x + 1) \) 的导数 \( f'(x) \)
分析:复合函数求导,外层为 \( \sinh u \),内层为 \( u = 2x + 1 \),先记双曲函数导数公式:\( (\sinh u)' = \cosh u \cdot u' \);
第一步:求外层导数:\( (\sinh u)' = \cosh u = \cosh(2x + 1) \);
第二步:求内层导数:\( u' = (2x + 1)' = 2 \);
第三步:乘积得:\( f'(x) = \cosh(2x + 1) \cdot 2 = 2\cosh(2x + 1) \)。
结论:\( f'(x) = 2\cosh(2x + 1) \)。
例题8:求函数 \( f(x) = \cosh^2 x \) 的导数 \( f'(x) \)
分析:复合函数求导,外层为 \( u^2 \)(\( u = \cosh x \)),先记 \( (\cosh u)' = \sinh u \cdot u' \);
第一步:外层导数:\( (u^2)' = 2u = 2\cosh x \);
第二步:内层导数:\( u' = (\cosh x)' = \sinh x \);
第三步:乘积得:\( f'(x) = 2\cosh x \cdot \sinh x = \sinh 2x \)(利用例题4的恒等式 \( \sinh 2x = 2\sinh x \cosh x \) 化简)。
结论:\( f'(x) = \sinh 2x \)。
例题9:求函数 \( f(x) = \tanh(\ln x) \) 的导数 \( f'(x) \)(\( x > 0 \))
分析:复合函数求导,外层为 \( \tanh u \),内层为 \( u = \ln x \),双曲正切导数公式:\( (\tanh u)' = \text{sech}^2 u \cdot u' \);
第一步:外层导数:\( (\tanh u)' = \text{sech}^2 u = \text{sech}^2(\ln x) \);
第二步:内层导数:\( u' = (\ln x)' = \frac{1}{x} \);
第三步:化简 \( \text{sech}^2(\ln x) \):因 \( \text{sech} u = \frac{1}{\cosh u} \),故 \( \text{sech}^2(\ln x) = \frac{1}{\cosh^2(\ln x)} \),由例题2知 \( \cosh(\ln x) = \frac{x^2 + 1}{2x} \)(代入 \( x \) 替换 \( 2 \)),故 \( \cosh^2(\ln x) = \left( \frac{x^2 + 1}{2x} \right)^2 \),因此 \( \text{sech}^2(\ln x) = \frac{4x^2}{(x^2 + 1)^2} \);
最终导数:\( f'(x) = \frac{4x^2}{(x^2 + 1)^2} \cdot \frac{1}{x} = \frac{4x}{(x^2 + 1)^2} \)。
结论:\( f'(x) = \frac{4x}{(x^2 + 1)^2} \)。
例题10:解方程 \( \sinh x + \cosh x = e^x \)
分析:代入双曲函数定义,左边化简后与右边对比:
左边:\( \sinh x + \cosh x = \frac{e^x - e^{-x}}{2} + \frac{e^x + e^{-x}}{2} = \frac{2e^x}{2} = e^x \);
右边:\( e^x \)。
结论:方程对所有 \( x \in \mathbb{R} \) 成立,解为 \( \mathbb{R} \)。
例题11:解方程 \( \cosh x - \sinh x = e^{-x} \)
分析:类似例题10,代入定义化简:
左边:\( \cosh x - \sinh x = \frac{e^x + e^{-x}}{2} - \frac{e^x - e^{-x}}{2} = \frac{2e^{-x}}{2} = e^{-x} \);
右边:\( e^{-x} \)。
结论:方程对所有 \( x \in \mathbb{R} \) 成立,解为 \( \mathbb{R} \)。
例题12:解方程 \( \tanh x = \frac{1}{2} \)
分析:利用双曲正切定义,转化为指数方程求解:
由 \( \tanh x = \frac{e^x - e^{-x}}{e^x + e^{-x}} = \frac{1}{2} \),交叉相乘得:\( 2(e^x - e^{-x}) = e^x + e^{-x} \);
整理:\( 2e^x - 2e^{-x} - e^x - e^{-x} = 0 \Rightarrow e^x - 3e^{-x} = 0 \);
两边乘 \( e^x \)(\( e^x > 0 \),不改变方程解):\( e^{2x} - 3 = 0 \Rightarrow e^{2x} = 3 \);
取自然对数:\( 2x = \ln 3 \Rightarrow x = \frac{1}{2}\ln 3 = \ln \sqrt{3} \)。
结论:方程的解为 \( x = \ln \sqrt{3} \)。
例题13:求 \( \text{arsinh } 0 \) 的值
分析:代入反双曲正弦定义:\( \text{arsinh } x = \ln(x + \sqrt{x^2 + 1}) \);
\( \text{arsinh } 0 = \ln(0 + \sqrt{0^2 + 1}) = \ln(1) = 0 \)。
结论:\( \text{arsinh } 0 = 0 \)。
例题14:求 \( \text{arcosh } 1 \) 的值
分析:代入反双曲余弦定义,注意定义域 \( x \geq 1 \):
\( \text{arcosh } 1 = \ln(1 + \sqrt{1^2 - 1}) = \ln(1 + 0) = \ln 1 = 0 \)。
结论:\( \text{arcosh } 1 = 0 \)。
例题15:求 \( \text{artanh } \frac{1}{2} \) 的值
分析:代入反双曲正切定义,定义域 \( (-1, 1) \),\( \frac{1}{2} \in (-1, 1) \):
\( \text{artanh } \frac{1}{2} = \frac{1}{2}\ln\left( \frac{1 + \frac{1}{2}}{1 - \frac{1}{2}} \right) = \frac{1}{2}\ln\left( \frac{\frac{3}{2}}{\frac{1}{2}} \right) = \frac{1}{2}\ln 3 \)。
结论:\( \text{artanh } \frac{1}{2} = \frac{1}{2}\ln 3 \)。
例题16:求 \( \text{arcoth } 2 \) 的值
分析:代入反双曲余切定义,定义域 \( (1, +\infty) \),\( 2 \in (1, +\infty) \):
\( \text{arcoth } 2 = \frac{1}{2}\ln\left( \frac{2 + 1}{2 - 1} \right) = \frac{1}{2}\ln\left( \frac{3}{1} \right) = \frac{1}{2}\ln 3 \)。
结论:\( \text{arcoth } 2 = \frac{1}{2}\ln 3 \)。
例题17:化简表达式 \( \text{arsinh}(\sinh x) \)
分析:利用反函数的性质“若函数严格单调,则 \( f^{-1}(f(x)) = x \)”;
\( \sinh x \) 在 \( \mathbb{R} \) 上严格递增,故其反函数 \( \text{arsinh} x \) 满足 \( \text{arsinh}(\sinh x) = x \)(对所有 \( x \in \mathbb{R} \) 成立)。
结论:\( \text{arsinh}(\sinh x) = x \)(\( x \in \mathbb{R} \))。
例题18:化简表达式 \( \text{arcosh}(\cosh x) \)
分析:\( \cosh x \) 在 \( [0, +\infty) \) 上严格递增,故反函数 \( \text{arcosh} x \) 的定义域为 \( [1, +\infty) \),值域为 \( [0, +\infty) \);
当 \( x \in [0, +\infty) \) 时,\( \cosh x \) 是原函数的严格递增部分,故 \( \text{arcosh}(\cosh x) = x \);
当 \( x \in (-\infty, 0] \) 时,因 \( \cosh x = \cosh(-x) \)(偶函数),且 \( -x \in [0, +\infty) \),故 \( \text{arcosh}(\cosh x) = \text{arcosh}(\cosh(-x)) = -x \);
综合得:\( \text{arcosh}(\cosh x) = |x| \)。
结论:\( \text{arcosh}(\cosh x) = |x| \)(\( x \in \mathbb{R} \))。
例题19:求函数 \( f(x) = \text{arsinh}(x^2) \) 的导数 \( f'(x) \)
分析:复合函数求导,外层为 \( \text{arsinh} u \),内层为 \( u = x^2 \),先记反双曲正弦导数公式:\( (\text{arsinh} u)' = \frac{1}{\sqrt{u^2 + 1}} \cdot u' \);
第一步:外层导数:\( (\text{arsinh} u)' = \frac{1}{\sqrt{u^2 + 1}} = \frac{1}{\sqrt{(x^2)^2 + 1}} = \frac{1}{\sqrt{x^4 + 1}} \);
第二步:内层导数:\( u' = (x^2)' = 2x \);
乘积得:\( f'(x) = \frac{1}{\sqrt{x^4 + 1}} \cdot 2x = \frac{2x}{\sqrt{x^4 + 1}} \)。
结论:\( f'(x) = \frac{2x}{\sqrt{x^4 + 1}} \)。
例题20:求函数 \( f(x) = \text{artanh}(\sin x) \) 的导数 \( f'(x) \)(需满足定义域 \( |\sin x| < 1 \),即 \( x \neq \frac{\pi}{2} + k\pi, k \in \mathbb{Z} \))
分析:复合函数求导,外层为 \( \text{artanh} u \),内层为 \( u = \sin x \),反双曲正切导数公式:\( (\text{artanh} u)' = \frac{1}{1 - u^2} \cdot u' \);
第一步:外层导数:\( (\text{artanh} u)' = \frac{1}{1 - u^2} = \frac{1}{1 - \sin^2 x} = \frac{1}{\cos^2 x} \)(利用三角恒等式 \( 1 - \sin^2 x = \cos^2 x \));
第二步:内层导数:\( u' = (\sin x)' = \cos x \);
乘积得:\( f'(x) = \frac{1}{\cos^2 x} \cdot \cos x = \frac{1}{\cos x} = \sec x \)。
结论:\( f'(x) = \sec x \)(\( x \neq \frac{\pi}{2} + k\pi, k \in \mathbb{Z} \))。
总结:双曲函数与反双曲函数的要点:
1. 定义是基础:所有性质(奇偶性、恒等式)和应用(求值、求导)均源于指数函数定义,需牢记6个双曲函数和4个常用反双曲函数的定义;
2. 恒等式是关键:\( \cosh^2 x - \sinh^2 x = 1 \)、\( \sinh 2x = 2\sinh x \cosh x \) 等恒等式是化简、求值的核心工具,注意与三角函数恒等式的符号差异;
3. 反函数需关注定义域:反双曲函数的定义域由原双曲函数的值域决定(如 \( \text{arcosh} x \) 定义域 \( [1, +\infty) \)),化简时需结合原函数的单调性(如 \( \text{arcosh}(\cosh x) = |x| \));
4. 求导公式要熟练:双曲函数导数与三角函数类似(\( \sinh' x = \cosh x \)、\( \cosh' x = \sinh x \)),反双曲函数导数可通过对数形式推导,无需死记硬背。
数学基础 : 小学数学、初中数学、高中数学、高等数学
- 函数同构问题:形式统一,单调性搭桥
- 映射、函数:\( f: A \to B \)
- 函数的定义域:Df
- 函数的值域:Rf
- 函数的解析式:f(x)
- 抽象函数:定义域、值域、解析式
- 分段函数:定义域、值域、单调性
- 复合函数: y = f[g(x)]
- 反函数:严格单调函数
- 隐函数:F(x, y) = 0
- 函数的有界性:\( |f(x)| \leq M \)
- 函数的单调性:增函数、减函数
- 函数的奇偶性:奇函数、偶函数
- 函数的周期性:\( f(x + T) = f(x) \)
- 类周期性:\(f(x+T)=f(x)+g(x)\)
- 函数的对称性:自对称、互对称
- 函数的凹凸性:凹函数、凸函数
- 图象平移、对称、翻折、缩放、旋转
- 函数的极值、函数的最值
- 二次函数:最值、根的分布、恒成立问题
- 三次函数:\( f(x) = ax^3 + bx^2 + cx + d \)
- 幂函数: \(y = x^a\)
- 对勾函数与双刀函数
- 指数方程:\(a^{x}=b\)(\(a > 0\)且\(a\neq1\))
- 指数函数:\(y = a^{x}(a>0\),且\(a\neq1)\)
- 双曲函数与反双曲函数
- 对数函数:对数运算性质
- 导数同构与导数异构
- 角度制与弧度制、弧长公式
- 三角函数:定义、性质
- 三角函数:诱导公式、恒等变换、辅助角
- 反三角函数:\(\arcsin x\)
- 三角函数二级结论
- 三角形内角的三角函数
- 数学中各类角的范围速记表
- 极坐标:\((\rho,\theta)\)=(极径,极角)
- 参数方程
- 等差数列
- 等比数列
- 数学归纳法
- 求和符号(∑ )、连乘符号(∏)
- 数列极限、函数极限、两个重要极限
- 函数的连续性:间断点、运算法则
- 函数的导数
- 函数的图形
- 函数的微分
- 罗尔定理、拉格朗日、柯西中值定理
- 无穷小、无穷大、洛必达法则求极限
- 泰勒公式、麦克劳林公式
- 弧微分、曲率、渐屈线、渐伸线、摆线
