指数函数:\(y = a^{x}(a>0\),且\(a\neq1)\)
一、指数函数的定义
一般地,函数\(y = a^{x}(a>0\),且\(a\neq1)\)叫做指数函数,其中\(x\)是自变量,函数的定义域是\(R\)。
例如,\(y = 2^{x}\)、\(y=\left(\frac{1}{3}\right)^{x}\)都是指数函数。这里要注意指数函数的底数\(a\)的取值范围是\(a>0\)且\(a\neq1\),因为当\(a = 0\)时,若\(x>0\),\(a^{x}=0\);若\(x\leqslant0\),\(a^{x}\)无意义。当\(a<0\)时,\(a^{x}\)的值在\(x\)取某些值(如分数)时无意义,而当\(a = 1\)时,\(y = 1^{x}=1\)是一个常数函数,不符合指数函数的定义。
二、指数函数的图象和性质
图象:
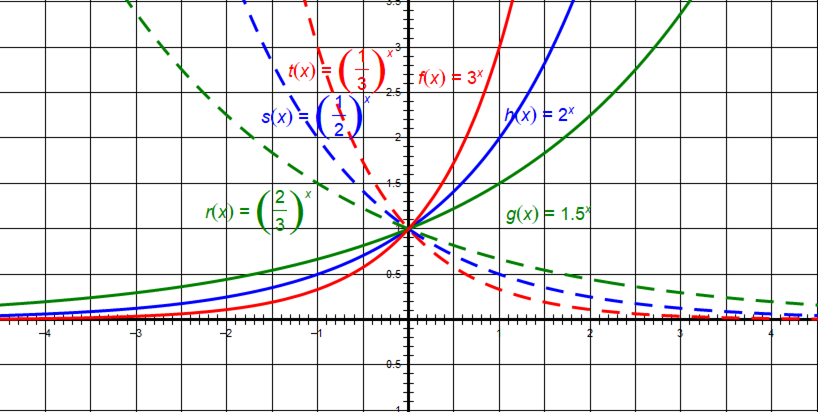
当\(a>1\)时,指数函数\(y = a^{x}\)的图象是上升的曲线。
例如,\(y = 2^{x}\)的图象,它经过点\((0,1)\),随着\(x\)的增大,\(y\)的值增长得越来越快。
当\(0<a<1\)时,指数函数\(y = a^{x}\)的图象是下降的曲线。
例如,\(y=\left(\frac{1}{2}\right)^{x}\)的图象,同样经过点\((0,1)\),随着\(x\)的增大,\(y\)的值逐渐减小,趋近于\(0\)。
性质:
定义域:指数函数的定义域是\(R\),这意味着\(x\)可以取任意实数。
例如,对于\(y = 3^{x}\),\(x\)可以是整数、分数、无理数等任何实数。
值域:当\(a>0\)且\(a\neq1\)时,指数函数的值域是\((0,+\infty)\)。因为对于任何实数\(x\),\(a^{x}>0\)。
例如,\(y = 5^{x}\),无论\(x\)取何值,\(y\)的值总是大于\(0\)的。
单调性:当\(a>1\)时,函数在\(R\)上单调递增;当\(0<a<1\)时,函数在\(R\)上单调递减。
例如,\(y = 2^{x}\)是单调递增函数,若\(x_{1}<x_{2}\),则\(2^{x_{1}}<2^{x_{2}}\);
例如,\(y=\left(\frac{1}{3}\right)^{x}\)是单调递减函数,若\(x_{1}<x_{2}\),则\(\left(\frac{1}{3}\right)^{x_{1}}>\left(\frac{1}{3}\right)^{x_{2}}\)。
过定点:指数函数\(y = a^{x}\)恒过定点\((0,1)\)。因为当\(x = 0\)时,\(a^{0}=1\)(\(a>0\)且\(a\neq1\))。
三、指数函数的定义中为什么要求a>0,且a≠1
1. 当\(a = 0\)时的情况
若\(x>0\),那么\(a^{x}=0^{x}=0\);但是若\(x\leqslant0\),\(0^{x}\)就无意义。例如,\(0^{-1}=\frac{1}{0}\)是不被允许的,因为在数学中除数不能为\(0\)。所以\(a = 0\)不符合指数函数对\(x\)取任意实数都有意义的要求。
2. 当\(a<0\)时的情况
当\(x\)是整数时,\(a^{x}\)是有意义的。例如,当\(a=-2\),\(x = 3\)时,\(a^{x}=(-2)^{3}=-8\)。
然而,当\(x\)是分数时,\(a^{x}\)可能会无意义。比如\(a = - 2\),\(x=\frac{1}{2}\),那么\(a^{x}=(-2)^{\frac{1}{2}}=\sqrt{-2}\),在实数范围内,负数不能开平方,所以此时函数值无意义。这样就无法保证对于任意的实数\(x\),函数\(y = a^{x}\)都有意义。
3. 当\(a = 1\)时的情况
此时函数\(y = 1^{x}=1\),对于任意的\(x\in R\),函数值始终为\(1\),这是一个常数函数。而指数函数要求它的底数\(a\)能够使函数值随着\(x\)的变化而变化,所以\(a = 1\)不符合指数函数的定义。
综上,为了保证函数\(y = a^{x}\)对于任意实数\(x\)都有意义,并且函数值能够随着\(x\)的变化而变化,指数函数的定义中要求\(a>0\),且\(a\neq1\)。
例题1. 判断是否为指数函数:下列函数中,哪些是指数函数?①\(y=2^{x}\);②\(y=x^{2}\);③\(y=(-2)^{x}\);④\(y=2^{x+1}\);⑤\(y=3^{-x}\)。
解析:
①是(符合\(y=a^{x}\)标准形式,\(a=2>1\));②不是(底数是变量\(x\),是幂函数);③不是(底数\(-2<0\),不符合定义);④不是(可变形为\(y=2×2^{x}\),多了系数2,非标准形式);⑤是(可变形为\(y=(\frac{1}{3})^{x}\),\(a=\frac{1}{3}∈(0,1)\),符合定义)。
例题2. 求定义域:求函数\(y=2^{\sqrt{x-1}}\)的定义域。
解析:
根号下的表达式需非负,即\(x-1≥0\),解得\(x≥1\),故定义域为\([1, +∞)\)。
例题3. 求值域:求函数\(y=3^{x}+1\)的值域。
解析:
由指数函数性质,\(3^{x}>0\),两边加1得\(3^{x}+1>1\),故值域为\((1, +∞)\)。
例题4. 求定点:求函数\(y=2^{x-3}+4\)过的定点坐标。
解析:
指数函数过定点的核心是“指数部分为0时,函数值恒定”。令\(x-3=0\),得\(x=3\),此时\(y=2^{0}+4=1+4=5\),故定点为\((3,5)\)。
例题5. 判断单调性:判断函数\(y=(\frac{2}{3})^{2x}\)的单调性。
解析:
先变形为\(y=[(\frac{2}{3})^{2}]^{x}=(\frac{4}{9})^{x}\),底数\(\frac{4}{9}∈(0,1)\),故函数在\(R\)上单调递减。
例题6. 比较函数值大小:已知\(a=2^{0.3}\),\(b=2^{0.5}\),\(c=(\frac{1}{2})^{0.4}\),比较\(a\)、\(b\)、\(c\)的大小。
解析:
先统一底数,\(c=(\frac{1}{2})^{0.4}=2^{-0.4}\);因\(y=2^{x}\)单调递增,且\(-0.4<0.3<0.5\),故\(2^{-0.4}<2^{0.3}<2^{0.5}\),即\(c<a<b\)。
例题7. 根据单调性求参数范围:已知函数\(y=(a^{2}-3a+3)a^{x}\)是单调递增的指数函数,求\(a\)的值。
解析:
第一步,指数函数需满足“系数为1”,即\(a^{2}-3a+3=1\),解得\(a=1\)或\(a=2\);第二步,排除\(a=1\)(因\(a≠1\)),且\(a=2>1\)时函数单调递增,故\(a=2\)。
例题8. 图像平移问题:将指数函数\(y=2^{x}\)的图像向右平移2个单位,再向上平移3个单位,得到的新函数解析式是什么?
解析:
函数图像平移遵循“左加右减、上加下减”(针对\(x\)的变化是“左加右减”,针对函数值的变化是“上加下减”)。向右平移2个单位得\(y=2^{x-2}\),再向上平移3个单位得\(y=2^{x-2}+3\)。
例题9. 解指数方程:解方程\(4^{x}-2^{x+1}-3=0\)。
解析:
用换元法,令\(t=2^{x}(t>0)\),则\(4^{x}=(2^{2})^{x}=t^{2}\),方程变为\(t^{2}-2t-3=0\);因式分解得\((t-3)(t+1)=0\),解得\(t=3\)或\(t=-1\)(舍去\(t=-1\),因\(t>0\));故\(2^{x}=3\),解得\(x=log_{2}3\)(若未学对数,可保留“\(x=log_{2}3\)”的形式)。
例题10. 解指数不等式:解不等式\((\frac{1}{3})^{x-1}>9\)。
解析:
统一底数,\(9=3^{2}=(\frac{1}{3})^{-2}\),不等式变为\((\frac{1}{3})^{x-1}>(\frac{1}{3})^{-2}\);因\(y=(\frac{1}{3})^{x}\)单调递减,故“不等号方向反转”,得\(x-1<-2\),解得\(x<-1\)。
例题11. 定义域与单调性结合:求函数\(y=(\frac{1}{2})^{x^{2}-2x}\)的单调递增区间。
解析:
用“复合函数单调性”(同增异减),令\(u=x^{2}-2x\)(内层函数),则\(y=(\frac{1}{2})^{u}\)(外层函数,单调递减);故内层函数单调递减的区间,即为复合函数单调递增的区间。\(u=x^{2}-2x\)是二次函数,对称轴为\(x=1\),单调递减区间为\((-∞,1]\),故原函数的单调递增区间为\((-∞,1]\)。
例题12. 值域与二次函数结合:求函数\(y=2^{x^{2}-4x+3}\)的值域。
解析:
令\(u=x^{2}-4x+3\),先求\(u\)的值域:\(u=(x-2)^{2}-1≥-1\);再看外层函数\(y=2^{u}\)(单调递增),故当\(u≥-1\)时,\(2^{u}≥2^{-1}=\frac{1}{2}\),即原函数的值域为\([\frac{1}{2}, +∞)\)。
例题13. 奇偶性判断:判断函数\(f(x)=2^{x}+2^{-x}\)的奇偶性。
解析:
第一步,定义域为\(R\),关于原点对称;第二步,计算\(f(-x)\):\(f(-x)=2^{-x}+2^{x}=f(x)\),故函数为偶函数。
例题14. 实际应用(增长率问题):某公司初始资金为100万元,资金年增长率为5%,按复利计算(即每年的资金是上一年的1.05倍),求5年后的资金总额(精确到0.1万元)。
解析:
复利问题对应指数函数模型\(y=P(1+r)^{x}\),其中\(P=100\)(初始资金),\(r=5\%=0.05\)(增长率),\(x=5\)(年数)。代入得\(y=100×1.05^{5}\),计算得\(1.05^{5}≈1.2763\),故\(y≈100×1.2763≈127.6\)万元。
例题15. 分段函数与指数函数结合:已知函数\(f(x)=\begin{cases}2^{x}, & x≥0 \\ (\frac{1}{2})^{x}, & x<0\end{cases}\),求\(f(-1)+f(1)\)的值。
解析:
\(f(-1)\)对应\(x<0\)的解析式,\(f(-1)=(\frac{1}{2})^{-1}=2\);\(f(1)\)对应\(x≥0\)的解析式,\(f(1)=2^{1}=2\);故\(f(-1)+f(1)=2+2=4\)。
例题16. 指数函数与方程根的个数:判断方程\(2^{x}=x+2\)的实数根个数。
解析:
通过“图像法”,分别画出\(y=2^{x}\)(过\((0,1)\),单调递增)和\(y=x+2\)(斜率为1的直线,过\((0,2)\)、\((2,4)\))的图像。观察交点:当\(x=-1\)时,\(2^{-1}=0.5\),\(x+2=1\),\(0.5<1\);当\(x=0\)时,\(2^{0}=1\),\(x+2=2\),\(1<2\);当\(x=1\)时,\(2^{1}=2\),\(x+2=3\),\(2<3\);当\(x=2\)时,\(2^{2}=4\),\(x+2=4\),相等(1个交点);当\(x=3\)时,\(2^{3}=8\),\(x+2=5\),\(8>5\);当\(x=-2\)时,\(2^{-2}=0.25\),\(x+2=0\),\(0.25>0\),故在\(x<-1\)处还有1个交点。综上,实数根个数为2。
例题17. 参数方程问题:已知关于\(x\)的方程\(a^{x}=x+1\)(\(a>0且a≠1\))有且只有一个解,求\(a\)的值。
解析:
结合图像分析,\(y=a^{x}\)与\(y=x+1\)恒过\((0,1)\)(\(a^{0}=1\),\(0+1=1\))。当\(a=1\)时不符合定义,排除;当\(a>1\)时,\(y=a^{x}\)在\(x=0\)处的切线斜率大于1(导数\(y’=a^{x}ln a\),\(x=0\)时斜率为\(ln a>0\)),仅在\((0,1)\)处有1个交点;当\(0<a<1\)时,\(y=a^{x}\)在\(x=0\)处的切线斜率为\(ln a<0\),除\((0,1)\)外,还会在\(x>0\)处有1个交点,不符合“只有一个解”;当\(a=e\)时(导数\(ln e=1\),切线与\(y=x+1\)重合),但实际\(a=1\)时才会有特殊情况,进一步验证:当\(a=1\)排除,当\(a=e\)时方程解为\(x=0\)(唯一),但更简单的是:当\(a=1\)不行,当\(a>1\)时唯一解在\(x=0\),当\(0<a<1\)时两个解,故\(a>1\)?不,实际当\(a=e^{\frac{1}{e}}\)时是临界值,此处简化:若方程只有一个解,必在\(x=0\),且函数在该点相切,导数相等,\(a^{0}ln a=1\)(\(y=x+1\)斜率为1),即\(ln a=1\),故\(a=e\)。
例题18. 不等式恒成立问题:若对任意\(x>0\),不等式\(2^{x}+m>0\)恒成立,求实数\(m\)的取值范围。
解析:
不等式变形为\(m>-2^{x}\)。因\(x>0\)时,\(2^{x}>2^{0}=1\),故\(-2^{x}<-1\);要使\(m>-2^{x}\)对任意\(x>0\)恒成立,需\(m≥-1\)(即\(m\)大于等于\(-2^{x}\)的最大值\(-1\))。
例题19. 指数函数与对数函数结合:已知\(2^{x}=3\),\(3^{y}=2\),求\(x+y\)的值。
解析:
由\(2^{x}=3\)得\(x=log_{2}3\),由\(3^{y}=2\)得\(y=log_{3}2\);根据对数性质\(log_{a}b×log_{b}a=1\),且\(x+y=log_{2}3+log_{3}2\),但更简单的是:两边取对数,\(x=ln3/ln2\),\(y=ln2/ln3\),故\(x+y=(ln²3 + ln²2)/(ln2ln3)\),但实际计算数值:\(x≈1.585\),\(y≈0.631\),故\(x+y≈2.216\),若保留符号形式,即为\(log_{2}3 + log_{3}2\)。
例题20. 抽象函数问题:已知函数\(f(x)\)满足\(f(x+y)=f(x)f(y)\),且\(f(1)=2\),求\(f(3)\)的值。
解析:
抽象函数满足指数函数的运算性质(\(a^{x+y}=a^{x}a^{y}\)),故可推测\(f(x)=2^{x}\)。验证:\(f(3)=f(2+1)=f(2)f(1)=[f(1+1)]f(1)=f(1)f(1)f(1)=2×2×2=8\),故\(f(3)=8\)。
数学基础 : 小学数学、初中数学、高中数学、高等数学
- 基于函数凹凸性的不等式缩放
- 函数同构问题:形式统一,单调性搭桥
- 映射、函数:\( f: A \to B \)
- 函数的定义域:Df
- 函数的值域:Rf
- 函数的解析式:f(x)
- 抽象函数:定义域、值域、解析式
- 分段函数:定义域、值域、单调性
- 复合函数: y = f[g(x)]
- 反函数:严格单调函数
- 隐函数:F(x, y) = 0
- 函数的有界性:\( |f(x)| \leq M \)
- 函数的单调性:增函数、减函数
- 函数的奇偶性:奇函数、偶函数
- 函数的周期性:\( f(x + T) = f(x) \)
- 类周期性:\(f(x+T)=f(x)+g(x)\)
- 函数的对称性:自对称、互对称
- 函数的凹凸性:凹函数、凸函数
- 图象平移、对称、翻折、缩放、旋转
- 函数的极值、函数的最值
- 二次函数:最值、根的分布、恒成立问题
- 三次函数:\( f(x) = ax^3 + bx^2 + cx + d \)
- 幂函数: \(y = x^a\)
- 对勾函数与双刀函数
- 指数方程:\(a^{x}=b\)(\(a > 0\)且\(a\neq1\))
- 指数函数:\(y = a^{x}(a>0\),且\(a\neq1)\)
- 双曲函数与反双曲函数
- 对数函数:对数运算性质
- 导数同构与导数异构
- 角度制与弧度制、弧长公式
- 三角函数:定义、性质
- 三角函数:诱导公式、恒等变换、辅助角
- 反三角函数:\(\arcsin x\)
- 三角函数二级结论
- 三角形内角的三角函数
- 数学中各类角的范围速记表
- 极坐标:\((\rho,\theta)\)=(极径,极角)
- 参数方程
- 等差数列
- 等比数列
- 数学归纳法
- 求和符号(∑ )、连乘符号(∏)
- 数列极限、函数极限
- 函数的连续性:间断点、运算法则
- 函数的导数
- 函数的图形
- 函数的微分
- 罗尔定理、拉格朗日、柯西中值定理
- 无穷小、无穷大、洛必达法则求极限
- 泰勒公式、麦克劳林公式
