三角形的旁心（Ia、Ib、Ic）

陈一男学习网站[ ChenYinan.com ] - 中国数学学会 - 中国院士 - GeoGebra - 数学基础

一、三角形的旁心

三角形的旁心，是指三角形一个内角的平分线与另外两个内角的外角平分线的交点。三角形共有3个旁心，分别对应三条边（每个旁心都与一条边“相对”，位于该边所在直线的外侧）。

在△ABC中：

与边BC相对的旁心（记为\(I_a\)）：是∠BAC的平分线与∠ABC的外角平分线、∠ACB的外角平分线的交点；

与边AC相对的旁心（记为\(I_b\)）：是∠ABC的平分线与∠BAC的外角平分线、∠ACB的外角平分线的交点；

与边AB相对的旁心（记为\(I_c\)）：是∠ACB的平分线与∠BAC的外角平分线、∠ABC的外角平分线的交点。

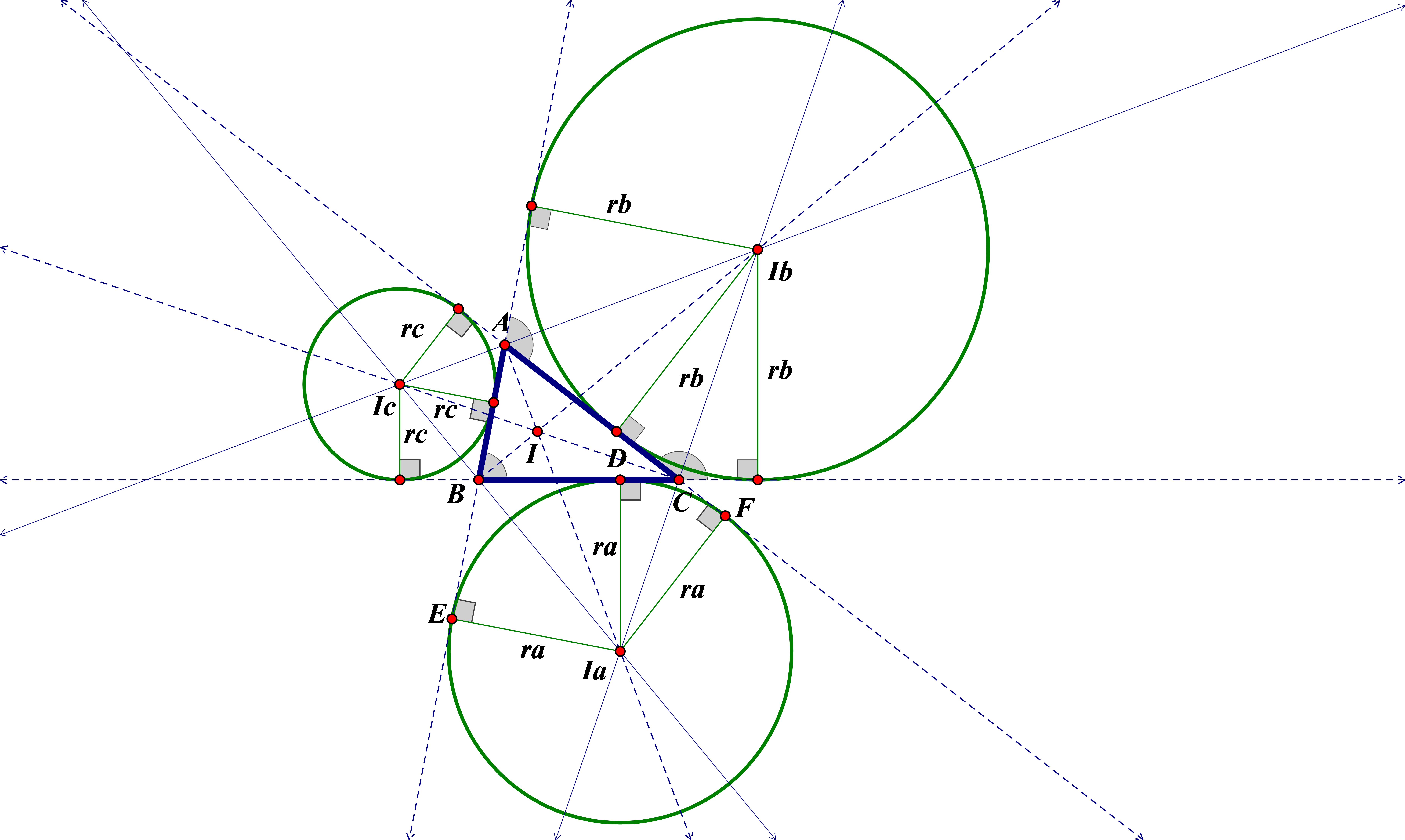
平面几何：三角形的旁心

二、三角形的旁心性质

1. 距离相等：任意一个旁心到三角形三条边所在直线的距离相等，这个距离称为旁切圆半径（记为\(r_a\)、\(r_b\)、\(r_c\)，分别对应旁心\(I_a\)、\(I_b\)、\(I_c\)的旁切圆半径）。

例如，旁心\(I_a\)到BC、AB延长线、AC延长线的距离都等于\(r_a\)。

2. 角的关系：设△ABC的内角为∠A、∠B、∠C，则：旁心\(I_a\)与内角的关系：\(∠BI_aC = 90° - \frac{1}{2}∠A\)；同理，\(∠AI_bC = 90° - \frac{1}{2}∠B\)，\(∠AI_cB = 90° - \frac{1}{2}∠C\)。

3. 切线长公式：若旁心\(I_a\)对应的旁切圆与BC相切于点D，与AB延长线相切于点E，与AC延长线相切于点F，则切线长满足：

\(AE = AF = \frac{1}{2}(AB + BC + AC) = s\)（其中\(s\)为△ABC的半周长，即\(s = \frac{a + b + c}{2}\)，\(a=BC\)，\(b=AC\)，\(c=AB\)）；

同时，\(BD = BE = s - b\)，\(CD = CF = s - c\)。

4. 旁切圆半径与面积的关系：△ABC的面积\(S\)与旁切圆半径的关系为\(S = r_a(s - a) = r_b(s - b) = r_c(s - c)\)（可类比内心的“\(S = r s\)”，但旁心对应“半周长减对边长度”）。

5. 共线性质：三角形的一个内角平分线与另外两个旁心共线（例如，∠A的平分线过\(I_b\)和\(I_c\)）；三个旁心与内心构成的四边形中，内心是三个旁心连线所成三角形的垂心。

三、三角形的旁心判定方法

若一个点满足以下条件之一，则该点是三角形的旁心：

1. 该点是三角形一个内角平分线与另外两个内角外角平分线的交点；

2. 该点到三角形三条边所在直线的距离相等，且位于三角形的外部（区别于内心——内心在三角形内部）。

例题1：基础概念辨析

判断下列说法是否正确，并说明理由：

（1）三角形的旁心在三角形内部；（2）一个三角形只有1个旁心；（3）旁心到三角形三条边的距离相等。

解析：

（1）错误。旁心是内角平分线与另外两个外角平分线的交点，外角平分线在三角形外部，因此旁心必在三角形外部；

（2）错误。一个三角形有3个旁心，分别对应三条边；

（3）正确。旁心的定义衍生性质：旁心到三条边所在直线的距离相等（即旁切圆半径）。

例题2：旁心与内角的角度计算（一）

在△ABC中，∠A=60°，求与边BC相对的旁心\(I_a\)满足的\(∠BI_aC\)的度数。

解析：

根据旁心的角关系性质：\(∠BI_aC = 90° - \frac{1}{2}∠A\)。

已知∠A=60°，代入得：\(∠BI_aC = 90° - \frac{1}{2}×60° = 90° - 30° = 60°\)。

故\(∠BI_aC = 60°\)。

例题3：旁心与内角的角度计算（二）

在△ABC中，旁心\(I_b\)满足\(∠AI_bC = 50°\)，求△ABC中∠B的度数。

解析：

根据旁心的角关系性质：\(∠AI_bC = 90° - \frac{1}{2}∠B\)。

已知\(∠AI_bC = 50°\)，代入得方程：\(50° = 90° - \frac{1}{2}∠B\)。

解方程：\(\frac{1}{2}∠B = 90° - 50° = 40°\)，故∠B = 80°。

例题4：切线长公式的应用（一）

已知△ABC的三边长度为AB=5，BC=6，AC=7，求与边BC相对的旁心\(I_a\)对应的旁切圆与AB延长线的切线长。

解析：

第一步，计算半周长\(s\)：\(s = \frac{AB + BC + AC}{2} = \frac{5 + 6 + 7}{2} = 9\)。

第二步，根据切线长公式：与\(I_a\)对应的旁切圆与AB延长线的切线长\(BE = s - AC\)（因AC=b=7，对应“s - b”）。

代入得：\(BE = 9 - 7 = 2\)。（或直接用“\(AE = s\)”，AE=AB + BE，即9=5 + BE，得BE=2，结果一致）。

例题5：切线长公式的应用（二）

在△ABC中，与边AC相对的旁心\(I_b\)对应的旁切圆与BC相切于点D，已知AB=4，AC=5，半周长\(s=8\)，求CD的长度。

解析：

第一步，先求BC的长度：由\(s = \frac{AB + BC + AC}{2} = 8\)，代入AB=4，AC=5，得\(\frac{4 + BC + 5}{2} = 8\)，解得BC=7（即a=7）。

第二步，根据切线长公式：与\(I_b\)对应的旁切圆与BC的切线长\(CD = s - AB\)（因AB=c=4，对应“s - c”）。

代入得：\(CD = 8 - 4 = 4\)。

例题6：旁切圆半径与面积的关系（一）

已知△ABC的面积S=24，半周长s=12，BC=8（即a=8），求与边BC相对的旁切圆半径\(r_a\)。

解析：

根据旁切圆半径与面积的关系：\(S = r_a(s - a)\)。

已知S=24，s=12，a=8，先计算\(s - a = 12 - 8 = 4\)。

代入公式得：\(24 = r_a×4\)，解得\(r_a = 6\)。

例题7：旁切圆半径与面积的关系（二）

在△ABC中，AB=5，BC=5，AC=6（等腰三角形），求与边AC相对的旁切圆半径\(r_b\)。

解析：

第一步，计算半周长\(s\)：\(s = \frac{5 + 5 + 6}{2} = 8\)。

第二步，计算面积S：等腰三角形AC边上的高h，由勾股定理得\(h = \sqrt{AB^2 - (\frac{AC}{2})^2} = \sqrt{5^2 - 3^2} = 4\)，故\(S = \frac{1}{2}×AC×h = \frac{1}{2}×6×4 = 12\)。

第三步，根据公式\(S = r_b(s - b)\)（AC=b=6，故\(s - b = 8 - 6 = 2\)）：

代入得\(12 = r_b×2\)，解得\(r_b = 6\)。

例题8：旁心、内心与角的综合计算

在△ABC中，内心为I，与边BC相对的旁心为\(I_a\)，证明：∠I\(I_a\)B = ∠I\(I_a\)C。

解析：

要证∠I\(I_a\)B = ∠I\(I_a\)C，只需证\(I_aI\)是∠BI\(I_a\)C的平分线，即证I在∠BI\(I_a\)C的平分线上，或利用角平分线的定义。

第一步，由旁心定义：\(I_a\)在∠ABC的外角平分线上，故\(I_aB\)平分∠ABC的外角；

由内心定义：I在∠ABC的平分线上，故IB平分∠ABC。

因此，∠IBA + ∠ABI\(I_a\) = \(\frac{1}{2}∠ABC + \frac{1}{2}(180° - ∠ABC)\) = 90°，即∠IB\(I_a\) = 90°。

第二步，同理，∠IC\(I_a\) = 90°（I在∠ACB的平分线上，\(I_a\)在∠ACB的外角平分线上）。

第三步，在四边形IB\(I_a\)C中，∠IB\(I_a\) = ∠IC\(I_a\) = 90°，且I、B、\(I_a\)、C四点共圆（对角互补）。

又因IB平分∠ABC，IC平分∠ACB，且\(I_a\)B、\(I_a\)C分别平分∠ABC、∠ACB的外角，可证IB = IC（等腰三角形或角平分线性质），故弧IB = 弧IC，对应圆周角∠I\(I_a\)B = ∠I\(I_a\)C。

综上，∠I\(I_a\)B = ∠I\(I_a\)C得证。

例题9：旁心与三角形形状的判断

在△ABC中，与边AB相对的旁心\(I_c\)满足\(∠AI_cB = 30°\)，且AB=AC，判断△ABC的形状。

解析：

第一步，由旁心角关系：\(∠AI_cB = 90° - \frac{1}{2}∠C\)（因\(I_c\)对应边AB，故关联内角∠C）。

已知\(∠AI_cB = 30°\)，代入得：\(30° = 90° - \frac{1}{2}∠C\)，解得∠C = 120°。

第二步，已知AB=AC，故△ABC是等腰三角形，且顶角∠C=120°，底角∠A=∠B = \(\frac{180° - 120°}{2}\) = 30°。

综上，△ABC是顶角为120°的等腰三角形。

例题10：旁心、切线长与周长的综合应用

已知△ABC的旁心\(I_a\)对应的旁切圆与BC相切于D，与AB延长线相切于E，若AE=10，BD=3，求△ABC的三边长度。

解析：

第一步，设△ABC的三边为BC=a，AC=b，AB=c，半周长\(s = \frac{a + b + c}{2}\)。

第二步，由切线长公式：

\(AE = AF = s = 10\)（已知AE=10，故s=10）；

\(BD = BE = s - b = 3\)（已知BD=3，故s - b = 3）。

第三步，推导各边关系：

由s=10，得\(a + b + c = 20\)（式1）；

由s - b = 3，得\(10 - b = 3\)，解得b=7（即AC=7）；

又因BE = s - b = 3，且BE = AE - AB = 10 - c，故10 - c = 3，解得c=7（即AB=7）；

将b=7、c=7代入式1，得a + 7 + 7 = 20，解得a=6（即BC=6）。

综上，△ABC的三边为AB=7，BC=6，AC=7。

数学基础 : 小学数学、初中数学、高中数学、高等数学